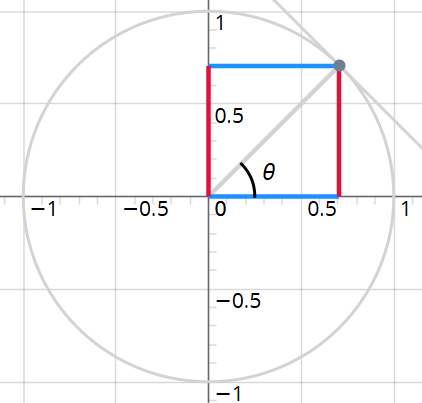
This is a self-contained course on trigonometry.
- Teacher: Daniel Deaconu

This is a self-contained course on trigonometry.

This course introduces students to Olympiad level knowledge on 3D geometry.
Basic ideas of trigonometry are required. (Sine Law, Cosine Law)

Topics covered:
Topics covered:

This course is intended for students with knowledge in counting/probabilities and it is meant to take students to an advanced level. Theoretical knowledge is assumed as known to the level of solving problems of the AMC12 level.

Topics covered:

This course provides all knowledge required for a student to be very familiar with the Binomial Theorem, important part of the curriculum required for math contests.

Topics covered:
Percentage problems

This is a self-contained course, whose purpose is to prepare students for success in the Grade 10 contests organised by U Waterloo.

This is a self-contained course preparing students for success in U Waterloo's Grade 11 contests.

This course is designed for students preparing for The Grace 9 contests organised by U Waterloo. It is a self contained course covering all topics assumed by the contests.

This course presents solution to more difficult problems from the CEMC contests for grades 9 and 10 and AMC10. Specific theoretical knowledge is presented in specialized courses in algebra, geometry, number theory and combinatorics, this particular course is mainly a problem solving course.
This course is intended for students getting ready for the Euclid contest and/or AMC12. The intermediate curse CEMC9-10-AMC10 provides a good coverage of the more basic ideas, but it is not a requirement.


This is a course that introduces students to the most advanced problems from the AMC8 curriculum.

This is a course based on the curriculum of the AMC8 contest. An introductory course in solving math problems, like AMC8 Level 1, would be a good background, but not mandatory.

This is a self contained course intended to introduce students to the curriculum of the AMC8 contest.

This course is an intermediate course based on the AMC10 curriculum.
It is a self-contained course whose goal is to enable students to qualify to AIME.

This is a self-contained course that introduces students to the AMC10 contest, Level 1. At the end of the course, students will be able to solve AMC10 level problems, roughly questions 1 to 13.